All Essential Vector Algebra Formulas PDF [100% Free]
Welcome to our comprehensive guide on vector algebra formulas! Whether you’re a student, educator, or just curious about vectors, this PDF compilation contains 100% free essential formulas to help you master vector concepts.
Physical Quantity: Property of a material or system that we can measure using numbers. These measurements have two important components:
- Magnitude: This represents the size or amount of the property.
- Unit: The unit gives meaning to the numerical value and allows us to compare and communicate data effectively.
There are mainly two type of physical quantity:
- Scalar Quantity: completely defined by only Magnitude.
- Vector Quantity: defined by Magnitude and Direction.
Vectors Representation/Notation
Vector Quantity has both Magnitude and Direction and must be follow vector algebra.
![]()
where A = magnitude of ![]() and
and ![]() = direction (unit vector)
= direction (unit vector)
Comparison between Scalar and Vector Quantity
| Scalar Quantity | Vector Quantity |
|---|---|
| Defined by only Magnitude | Magnitude + Direction |
| Follow Normal Algebraic Rules | Follow Vector Algebraic Rules |
| Scalar quantities are added, subtracted, or divided by Algebraically | Vector quantities are added and subtracted Geometrically |
| Examples: Length, Distance, Speed, Mass, Volume, Time, Time, Temperature, Work, Energy, Power, Electric Current, Charge, Potential, Flux, etc. | Examples: Position, Displacement, Velocity, Weight, Acceleration, Electric Field, Surface Area, Force, Torque, etc. |
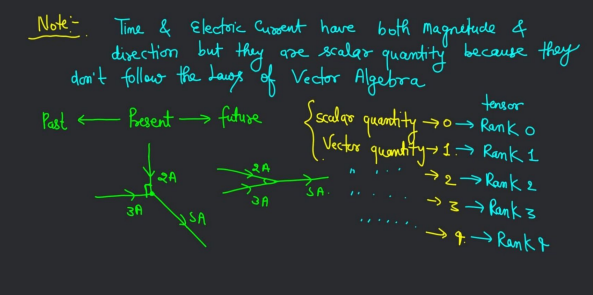
Physical Quantities having different values in different direction known as Tensor.
Examples: Moment of inertia, Refractive Index, Density Stress and Stain, etc.
Key Point:
Types of Vectors
| Sr.No. | Vector Type | Definition |
|---|---|---|
| 1. | Equal Vectors | Magnitudes |
| 2. | Opposite Vectors | Two vectors |
| 3. | Position Vector | |
| 4. | Displacement Vector | |
| 5. | Unit Vector | Magnitude: Unit (1), Direction: |
| 6. | Orthogonal Unit Vectors | The unit vector along x-axis |
| 7. | Zero / Null Vector ( | Magnitude: Zero (0) Direction: Arbitrary |
| 8. | Collinear Vectors | Two Parallel or Antiparallel vectors are called colinear vectors. |
| 9. | Coplanar Vectors | Vectors having same Plane or Parallel Plane are called coplanar. If |
| 10. | Polar Vector | These vectors have defined initial point. Examples: displacement, force, position, velocity, linear momentum..etc. |
| 11. | Axial Vector | These vectors always along an axis. Examples: angular momentum, angular velocity, torque, etc. |
Addition of Vectors
- Triangle Law of vector Addition: If two vectors A and B are represented as two sides of a triangle taken in order, then the third side of the triangle represents the resultant vector R:
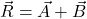
- Parallelogram law of vector addition: If two vectors A and B represented as adjacent sides of a parallelogram, then the diagonal of the parallelogram represents the resultant vector R:
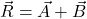
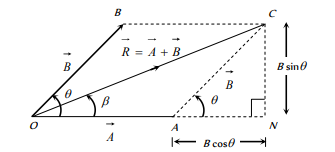
Magnitude of the Resultant Vector: ![]()
Direction of Resultant Vector: ![]()
| Case (1): If |
| Case (2): If |
| Case (3): If |
Subtraction of vectors
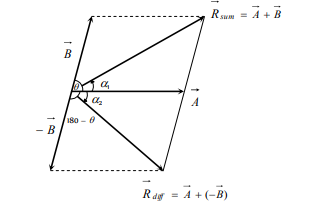
Magnitude of the Resultant Vector: ![]()
Direction of Resultant Vector: ![]()
| Case (1): If |
| Case (2): If |
| Case (3): If |
Formulas of Scalar Product of Two Vectors
If ![]() and
and ![]() having angle
having angle ![]() , then their scalar product is defined as:
, then their scalar product is defined as:
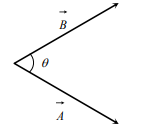
![]()
![]()
In terms of components, if ![]() and
and ![]()
![]()
| Case (1): If |
| Case (2): If |
Scalar Product Properties
- It is always a scalar.
- If
 (acute) then dot product always be positive.
(acute) then dot product always be positive. - If
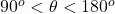 (obtuse) then dot product always be negative.
(obtuse) then dot product always be negative. 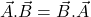 i.e. it is commutative.
i.e. it is commutative.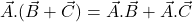 i.e. it is distributive.
i.e. it is distributive.- The scalar product of a vector by itself is termed as self dot product and is given by,
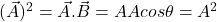 i.e.
i.e. 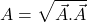
- The dot product of same orthogonal unit vectors :
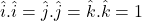
- The dot product of orthogonal unit vectors :
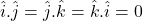
Examples of Scalar Product
- Work :
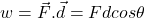
- Energy :
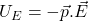 &
& 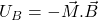
- Power :
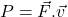
- Magnetic Flux :
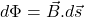
Formulas of Vector Product of Two Vectors
![]()
![]()
In terms of components: if ![]() and
and ![]()
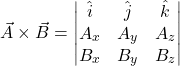
![]()
| Case (1): If |
| Case (2): If |
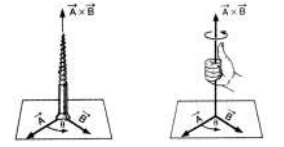
Vector Product Properties
- It is always a vector.
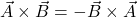 i.e. Vector product of two vectors is not commutative.
i.e. Vector product of two vectors is not commutative.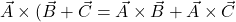 i.e. The vector product is distributive when the order of the vectors is strictly maintained.
i.e. The vector product is distributive when the order of the vectors is strictly maintained.- The self cross product, i.e., product of a vector by itself vanishes, i.e., is null vector
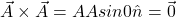
- The dot product of same orthogonal unit vectors :
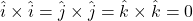
- The dot product of orthogonal unit vectors :
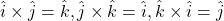
Examples of Cross products
Comparison between Scalar and Vector products
| Properties | Scalar Product | Vector Product |
|---|---|---|
| Formula | ||
| Commutative | ||
| Distributive | ||
